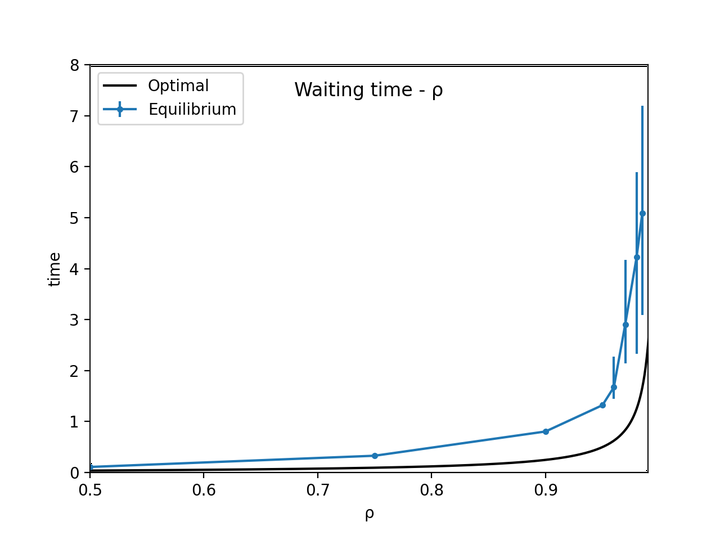
Comparison of the optimal expected waiting time (black) and the average waiting time of the found equilibrium (blue).People in today’s modern cities have been accustomed to the scene that thousands of people travels from uptown and suburban areas to downtown and urban areas every morning of workdays. This phenomena puts great stress on the traffic system, causing congestion at a specific period of a day, which is usually referred to as the morning peak. During morning peaks, bus stops and subway stations are filled with people who get up late and are hurrying up not to be late for work. Therefore, this competition for limited traffic resources among these workers naturally forms a game.
In this paper, a traffic game is formalize, abstracting the main features from this battle of peak hours. The ultimate goal of each player is to set off for work as late as possible while arriving before a deadline. To reflect the common rules of buses and subway systems, the traffic system adopts a first-come-first-serve(FCFS) rule with a fixed serving rate. Despite the inherent incontinuity of the ordering function exploited by FCFS rule, we show the existence of Nash equilibrium by modifying the original game with various approaches such as discretization or smoothing.
Aside from normal actions of queuing, a somewhat devious action, which we call detouring, is also taken into account. When Alice reaches a subway station and the queueis already very long, she may first travel in the reverse direction for several stops and then travels back, jumping the queue indirectly. Detouring may benefit some individuals, but it is a waste of the traffic capacity since the person travels longer. With more and more people adopting this strategy, social welfare diminishes. It is thus an example of the so-called ’involution’ that the pressure of competition leads to bad results on every individuals. In this paper, we analyze the behavior of detouring as a subgame with rules of M/D/1 queue model, incorporating corresponding conclusions from Queuing Theory.
While a Nash equilibrium is hard to find in general, we simulate these two games and successfully find $\epsilon$ Nash equilibrium in an iterative manner.
