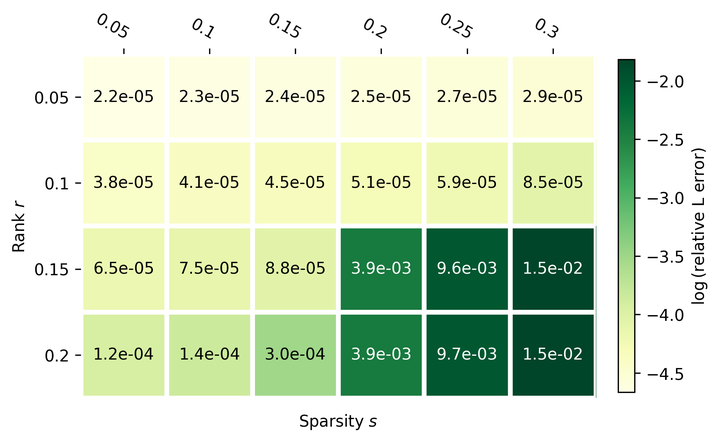
Relative recover error of different problem scales.
Principal component analysis (PCA) has been widely used for dimension reduction in data science. It extracts the top k significant components of a given matrix by computing the best low-rank approximation. However, it is well known that PCA is sensitive to noises and adversarial attacks. Robust PCA (RPCA) aims at mitigating this drawback by separating the noise out explicitly. Specifically, RPCA assumes that the observed matrix $M$ can be decomposed as $M = L^* + S^*$ where $L^*$ is a low-rank matrix and $S^*$ is a sparse matrix.
Some RPCA algorithms relax the low-rank constraints to nuclear norm and sparsity to $\ell_1$ norm, so that traditional convex optimization algorithms (e.g., PGM, ADMM) can be directly applied. Others reformulate the problem as low-rank matrix factorization with $\ell_1$ norm bounded noise. However, none of these algorithms are scalable and can be implemented distributedly, due to the use of SVD or full matrix multiplications. In this paper, we propose a distributed RPCA algorithm based on consensus-factorization (DCF-PCA) that takes $O(1)$ computation time as the number of remote clients increase. We show the convergence of our algorithm both theoretically and empirically.
